Contents
1. Introduction2. Keywords
3. Problem
4. Solution
5. Discussion
5.1 Power set
6. Practice: Generating a Power Set of a Given Set
7. Conclusions
8. Literature & Links
1. Introduction
We continue to discover the pretty amazing capabilities of LINQ as functional programming language. In this opportunity we are going to learn how to generate the power set of a given set. To learn this, we need to go back, i.e. to the previous recipe, and review how to generate partial permutations for a given set of elements. As we will verify soon, this practical knowledge is useful in discrete mathematics and consequently in computer science.
2. Keywords
- Discrete mathematics
- Functional programming
- Partial permutation
- Power set
- Set
3. Problem
Generate the power set of a given set.
4. Solution
Partial permutations are useful to generate the power set of a given set.
5. Discussion
5.1 Power set
In simple terms, a power set is a set of all subsets of a given set, including the empty set. By the same token, a power set is formally defined as
For example, if we have the set S with elements {x, y, z} its power set is equal to
{{}, {x}, {y}, {z}, {x, y}, {x, z}, {y, z}, {x, y, z}}
We can also compute the number of subsets of S with
where n is the number of elements in S. Hence, S has 8 subsets.
6. Practice: Generating a Power Set of a Given Set
It's time for LINQ and LINQPad! We are going to create a LINQ code implementation to compute the subsets of set -i.e., its power set-.
For the purpose of demonstrating this recipe, it's important to mention that the GeneratePartialPermutation(string) method from LINQ Recipe No. 2-14: How to Generate Permutations will be used to generate the partial permutations for the given set.
Then, these partial permutations will produce the element pairs to generate all the elements -sets- of the power set.
The GeneratePartialPermutation(string) method is declared in lines 2-6. It produces partial permutations for a given string of characters; for example, the "abc" has three partial permutations: "abc", "bac", and "cab".
Equally important, in lines 9-40, the Main method performs all these operations:
- Line 12: Set of characters to generate its power set.
- Line 15: Generates partial permutations for "abc".
- Lines 20-31: It creates the element pairs for each partial permutation.
- Lines 34-49:
- Line 35: Sorts each subset in ascending order.
- Line 37: Deduplicates subsets.
- Line 38: Sorts each subset by length in ascending order.
- Line 39: Outputs the resultant power set on LINQPad output window.
As an alternative code explanation, we have this short video tutorial with a execution demo:
7. Conclusions
This recipe has taught us how to generate the power set of a given set using a functional programming approach. At first it can appears messy, but once we understand the LINQ standard operators, the task is easy to accomplish.
Next recipe will teach us how to pick every element in an collection. That's will be pretty amazing!
8. Literature & Links
Mukherjee, S (2014). Thinking in LINQ Harnessing the Power of Functional Programming in .NET Applications. United States: Apress.Power set (2016, July 7). Retrieved from: https://en.wikipedia.org/wiki/Power_set
Power Set (2016, July 7). Retrieved from: https://www.mathsisfun.com/sets/power-set.html
Power Set (2016, July 7). Retrieved from: http://mathworld.wolfram.com/PowerSet.html
LINQ Recipe No. 2-14: How to Generate Permutations (2016, July 7). Retrieved from: https://ortizol.blogspot.com.co/2016/07/linq-recipe-no-2-14-how-to-generate-permutations.html
V
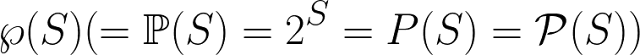

No hay comentarios:
Publicar un comentario
Envíe sus comentarios, dudas, sugerencias, críticas. Gracias.