LINQ Recipe No. 2-11: Recursive Series and Patterns - How to Generate Logo Command to Draw a Koch Curve

Contents

1. Introduction
2. Keywords
3. Problem
4. Solution
5. Discussion
5.1 L-system
5.2 Logo programming language and turtle graphics
6. Practice: Generate Logo Commands for Koch Curve Fractal
7. Conclusions
8. Literature & Links

1. Introduction

In the previous recipe we learned about the basic concepts to generate recursive series: in particular, we saw that the algae's growth is determined by a recursive formula which is described in terms of LINQ functional programming code. That's amazing. Now, in this recipe we will be discovering a new L-system and a series to generate Logo commands for drawing fractals -such as Koch Curve, Sierpinski Triangle, and Hilbert curve. We will also talk about the Logo: an fantastic programming language useful for learning programming.

2. Keywords

• Fractal
• Hilbert curve
• Koch Curve
• L-system
• Logo
• Recursive series
• Sierpinski triangle

3. Problem

Use LINQ to generate a Koch Curve.

4. Solution

In LINQ the programmer can implement an L-system to generate the recursive pattern for drawing a Koch Curve in terms of turtle graphics commands.

5. Discussion

5.1 L-system

An L-system (also known as Lindenmayer system) is defined as a formal grammar for generating well formed string formulas.

[Note: In LINQ Recipe No. 2-9: Recursive Series and Patterns-System Grammar the reader can find a more extensive and detailed overview of what is an L-system.]

5.2 Logo programming language and turtle graphics

The Logo programming language was designed to facilitate the learning of computer programming. It was created in 1967 ("Logo (programming language)", 2016), and was primarily designed to teach the fundamental programming concepts of Lisp programming language.

A key feature of this programming language was turtle graphics: a virtual onscreen turtle to draw shapes (Mukherjee, 2014). It basically consists of three attributes ("Turtle graphics", 2016): 

1. A location
2. An orientation: turn left, turn right.
3. A pen: 
1. Color
2. Width
3. Up and down

The user/programmer can move the turtle in terms of its relative position and orientation. For example, commands such as:

• Forward 15, 
• Turn right 90 degrees 

will be translated into "Move forward 15 spaces, and turn right 90 degrees".

A drawing system like turtle graphics is ideal to draw interesting and outstanding figures. The Koch curve is an example of a recursive pattern called fractal. A fractal is a figure generated by successive subdivisions.

In the next example fractal we can note that each successive subdivision is self-described as a whole structure but in minor scale: 

Illustration 1. Romanesco broccoli ("Earth's Most Stunning Natural Fractals Patterns", 2016).

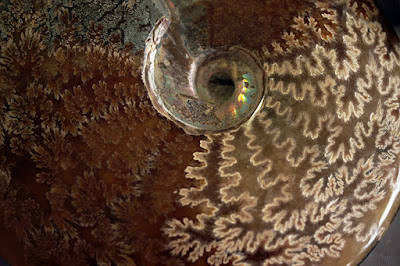Illustration 2. Ammonite sutures ("Earth's Most Stunning Natural Fractals Patterns", 2016).

Illustration 3. Snowflakes ("Earth's Most Stunning Natural Fractals Patterns", 2016).

6. Practice: Generate Logo Commands for Koch curve fractal

In this section we are going to explore how to generate the required commands, in Logo, to draw a Koch curve.

The first step consists in defining the formal system, i.e.:

• Variables: F
• Constants: +, -
• Start: F
• Rule: (F -> F+F-F-F+F)

The rule says: F must be replaced by F+F-F-F+F

By the other hand, the constants: + means turn right 90°, - means turn left 90°. And the variable F means draw forward.

Now we can implement this formal system using LINQ program elements: 

LINQ file KochCurve.linq [Alternative link][Alternative link]: 

Under the line 2 the string variable is declared to represent the Start value of the recursive pattern. Then, in line 5, the lambda expression x => x.Replace("F", "F+F-F-F+F"); is used to represent the replacement rule in each recursive iteration.

With the string variable command (lines 11-14), the turtle's initial location and direction is specified.

A recursive definition to generate the Logo commands is declared in lines 17-22:

• Line 17: Generates a range from 1 to 3. This range is to represent the three recursive iterations for the fractal.
• Line 18: Applies the transformation rule defined in line 5.
• Line 19: Gets the last transformation. It is a string with all three transformations processed.
• Lines 20-22: Performs all of the replacements to generate the final Logo commands.

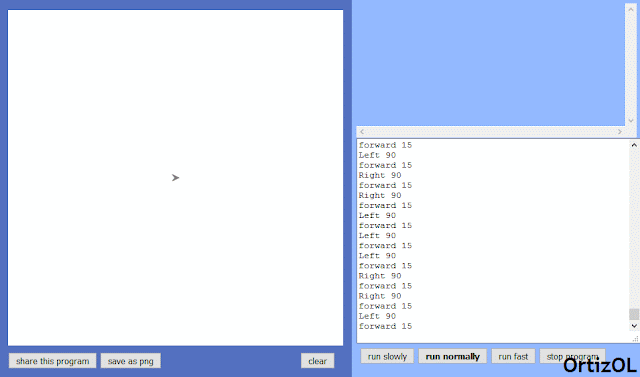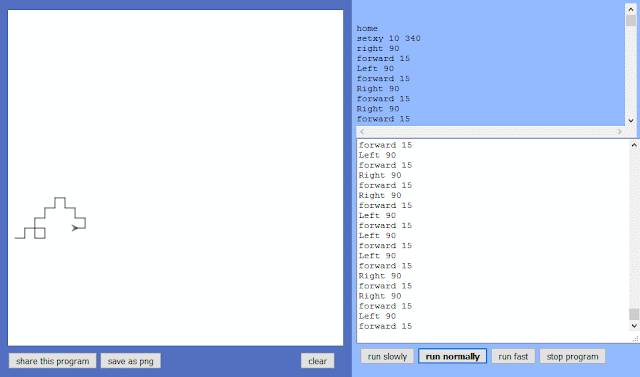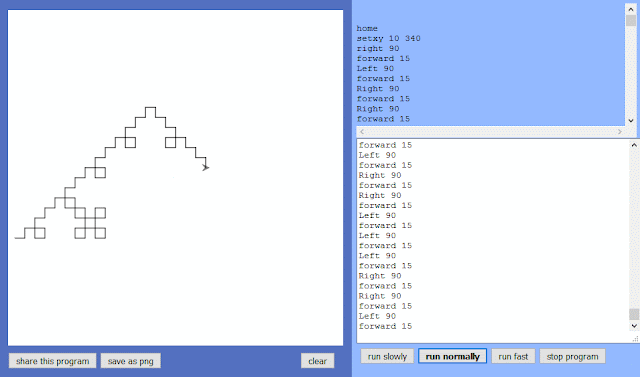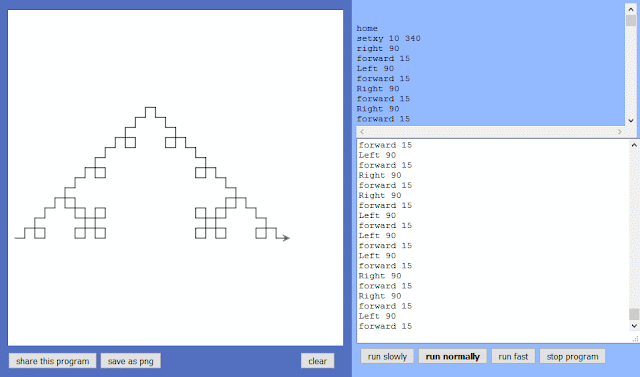
This tutorial give us a notion of LINQ code execution, and the generated Koch curve fractal: 

And this is the Koch curve: 

Animation 1. Koch curve fractal generation.

7. Conclusions

This has been an amazing opportunity to discover the incredible capabilities of LINQ as a functional programming language. The pattern recognition by an L-system approach allows us to write fractal throughout formal systems.

In the next LINQ recipe we will learn how to draw a Sierpinski Triangle using the same approach for this recipe.

8. Literature & Links

Mukherjee, S (2014). Thinking in LINQ Harnessing the Power of Functional Programming in .NET Applications. United States: Apress.
LINQ Recipe No. 2-9: Recursive Series and Patterns-System Grammar (2016, June 30). Retrieved from: https://ortizol.blogspot.com.co/2016/06/linq-recipe-no-2-9-recursive-series-and-patterns-how-to-generate-a-recursive-structure-via-l-system-grammar.html
Turtle graphics (2016, June 30). Retrieved from: https://en.wikipedia.org/wiki/Turtle_graphics
Logo (programming language) (2016, June 30). Retrieved from: https://en.wikipedia.org/wiki/Logo_(programming_language)
Earth’s Most Stunning Natural Fractal Patterns (2016, July 1). Retrieved from: http://www.wired.com/2010/09/fractal-patterns-in-nature/

V