LINQ Recipe No. 2-12: Recursive Series and Patterns: How to Generate Logo Commands to Draw a Sierpinski Triangle

Contents

1. Introduction
2. Keywords
3. Problem
4. Solution
5. Discussion
5.1 Sierpinski triangle
6. Practice: Drawing a Sierpinski Triangle using LOGO Commands
7. Conclusions
Literature & Links

1. Introduction

In this LINQ recipe we are going to draw another interesting and attractive fractal: the Sierpinski Triangle. Like in the previous recipe, we will be using LOGO commands to draw this fractal. This will require to implement a given pattern based on the L-system approach. Nature is full of beautiful and outstanding patterns that we, as programmers, can express using the amazing functional programming language LINQ. Let's get started!

2. Keywords

• Fractal
• L-System
• LINQ
• LOGO
• Sierpinski triangle

3. Problem

Draw the Sierpinski Triangle by using the L-system approach.

4. Solution

A new formal system based on L-system (also known as Lindenmayer system) will be used to express the recursive pattern to produce the necessary Logo commands for drawing the Sierpinski triangle fractal.

5. Discussion

5.1 Sierpinski triangle

This kind of fractal was described by the Polish mathematician Wacław Franciszek Sierpiński ("Wacław Sierpiński", 2016) in 1915 and appeared for first time in Italian art during the 13th century ("Sierpinski Sieve", 2016). It is also known as Sierpiński Sieve or Sierpinski gasket.

Illustration 1. Sierpinski triangle at different recursive phases.

The above picture shows the Sierpinski triangle at different recursive steps. The reader can note how the original, the first one, is implicitly reproduced in each of the fractal steps.

Additionally, this fractal is described by the following Lindenmayer system ("Sierpinski Sieve", 2016):

• Initial string: FXF--FF--FF
• Rewriting rules: 
• F → FF
• X → --FXF++FXF++FXF
• Angle: 60°

[Note: To learn more about this fractal, I recommend the lecture of this Wolfram MathWorld article: Sierpinski Sieve.]

6. Practice: Drawing a Sierpinski Triangle using Logo Commands

This LINQ implementation generates the necessary LOGO commands for drawing a Sierpinski triangle. But first we need to know about the Lindenmayer system (L-system) required to form the given fractal ("Mukherjee", 2016):

• Variables: A, B
• Constants: +, -
• Start: A
• Rules: (A → B-A-B), (B → A + B + A)
• Angle: 60º

The two variables are used to draw forward; the two constants + and - are used to turn left by some angle, and to turn right by some angle respectively.

[Note: In order to simplify the code explanation, we have used this L-system instead of the one explained in section 5.1.]

So let's get started coding: 

LINQ file SierpinskiTriangle.cs [Alternative link][Alternative link]: 

With the line 2 we declare/implement the starting value for the recursive pattern. Meanwhile, with lines 5-8 the replacement rules are specified; note in this case we have added an auxiliary transformation delegate called markBs (line 7); this is for avoiding the replacement of Bs for the next recursive step.

We set the int variable length to 6: this is number of steps for the recursive series (line 11).

The actual transformation is applied recursively in lines 14-17. The range 1-6 is converted into a List (line 15); after that, for each recursive step (range value) we store the transformation in the variable sierpinskiTriangle. (If you want to know how the transformation works, I recommend you to read this recipe  LINQ Recipe No. 2-9: Recursive Series and Patterns-System Grammar.)

Then, the LOGO commands are generated by string replacements in lines 20-21.

Finally, with line 27 the LOGO commands are output in the Result window (LINQPad): 

Illustration 2. LOGO commands for Sierpinski triangle.

Additionally, this video tutorial shows the step by step execution by using the LINQPad debugger:

And finally, an extra animation which shows how a Sierpinski triangle is drawn: 

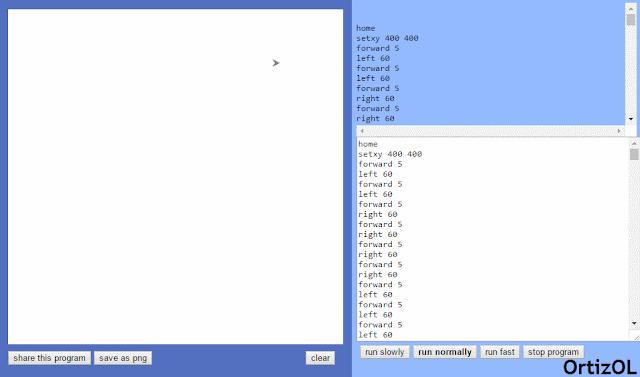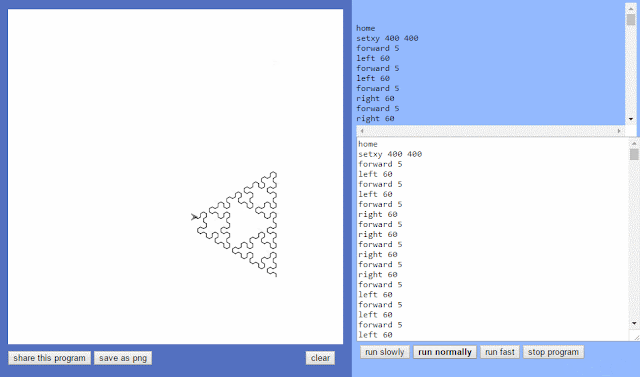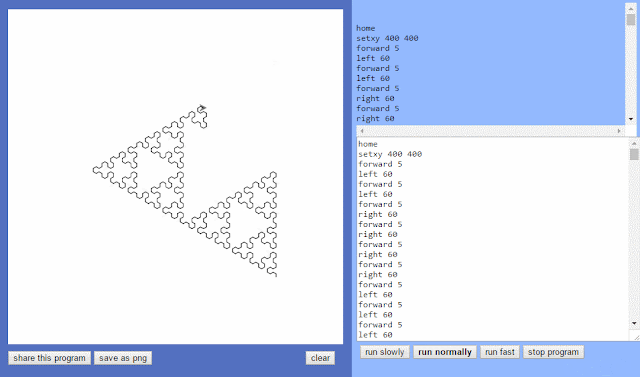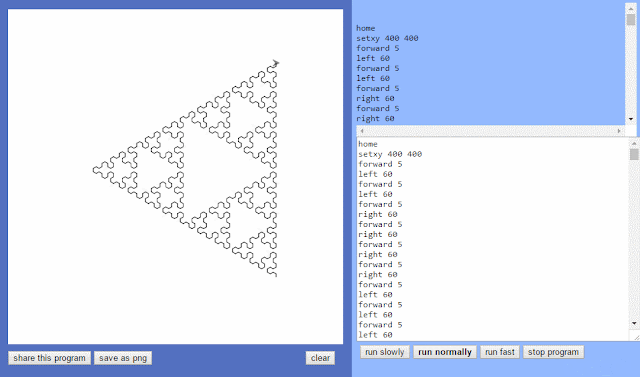Animation 1. Sierpinski triangle drawing.

7. Conclusions

We have learned that an L-system constitutes a formal way to express recursive figures like fractals.

Have you ever imagined an alternative way to generate Fibonacci numbers nonrecursively? We will have the opportunity, in the next LINQ recipe, to accomplish that using a functional programming approach.

8. Literature & Links

Mukherjee, S (2014). Thinking in LINQ Harnessing the Power of Functional Programming in .NET Applications. United States: Apress.
Wacław Sierpiński (2016, July 1). Retrieved from: https://en.wikipedia.org/wiki/Wac%C5%82aw_Sierpi%C5%84ski
Sierpiński Sieve (2016, July 1). Retrieved from: http://mathworld.wolfram.com/SierpinskiSieve.html
LINQ Recipe No. 2-9: Recursive Series and Patterns-System Grammar (2016, July 7). Retrieved from: https://ortizol.blogspot.com.co/2016/06/linq-recipe-no-2-9-recursive-series-and-patterns-how-to-generate-a-recursive-structure-via-l-system-grammar.html

V