LINQ Recipe No. 2-3: Mathematics and Statistics - How to Compute a Weighted Sum?

Contents

1. Introduction
2. Key Words
3. Problem
4. Solution
5. Discussion
5.1 Zip() standard query operator
5.2 Sum() standard query operator
5.3 Weighted sum
6. Practice: Compute the Weighted Sum for a Student's Score
Conclusions
Literature & Links

1. Introduction

In this third LINQ recipe -from the Series Generation-, we will learn how to compute the weighted sum: this type of sum, as we will see soon, is a dot product application; it basically allows to compute the sum of the coefficients of the vector dot product. To reinforce this important mathematical concept, we will present an example to compute the weight of the values obtained in an exam from multiple subjects.

2. Key Words

• Dot product
• LINQ
• Weighted sum

3. Problem

How to compute the weighted sum using LINQ standard query operators?

4. Solution

LINQ provides the Zip() and Sum() standard query operators to calculate easily the weighted sum.

5. Discussion

5.1 Zip() standard query operator

(Note: In LINQ recipe LINQ Recipe No. 2-1: Mathematics and Statistics - Compute the Dot Product of Two Vectors the Zip() standard query operator is explained in section 5.2.)

5.2 Sum() standard query operator

To compute the sum of a sequence of numeric values, the Sum() ("Enumerable.Sum Method", 2016) standard query operator is used. For example, to compute the sum of values generated from the Range ("Enumerable.Range Method", 2016) standard operator, the following code 

Enumerable.Range(1, 10).Sum().Dump("Sum from 1 to 10");

is a solution. Once it has been executed, it produces:

Illustration 1. Sum from 1 to 10 in LINQ.

5.3 Weighted sum

In the context of mathematics, the weighted sum is defined as the sum of the coefficients of the vector scalar product -or dot product- (Mukherjee, 2014).

Illustration 2. Weighted sum definition.

6. Practice: Compute the Weighted Sum for a Student's Score

We desire to compute the weighted sum of a student's score: in an exam, every subject evaluated has a different weight. In this particular case, each student's final score is the weighted sum defined as:

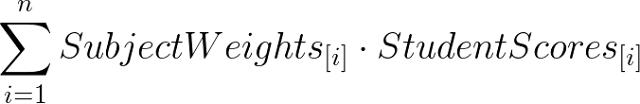Illustration 3. Weighted sum for a student's score.

This is the same as the sum of the weight for each subject multiplied by the score got by the student in that subject.

Now, the C# statements using LINQ standard query operators have this form:

int[] studentScores = {3, 4, 5, 3};

int[] subjectWeights = {5, 4, 4, 5};

studentScores.Zip(subjectWeights, (score, weight) =>

score * weight) // Dot product

.Sum() // Weighted sum

.Dump("Weighted Sum");

The resultant weighted sum is 

Illustration 4. Weighted sum for subject weights and student scores.

7. Conclusions

We have had the opportunity to learn how the weighted sum is computed using two of the standard query operators available in LINQ: Zip() and Sum(). The example in section 6 showed us how these two operators can be used to calculate the weighted sum of each subject and the score obtained in that subject.

In the next LINQ recipe we will learn how to find the percentile for each element in an array of numbers.

8. Literature & Links

Mukherjee, S (2014). Thinking in LINQ Harnessing the Power of Functional Programming in .NET Applications. United States: Apress.
LINQ Recipe No. 2-1: Mathematics and Statistics - Compute the Dot Product of Two Vectors (2016, March 22). Retrieved from: http://ortizol.blogspot.com.co/2016/03/linq-recipe-no-2-1-mathematics-and-statistics-compute-the-dot-product-of-two-vectors.html
Enumerable.Sum Method (System.Linq) (2016, March 22). Retrieved from: https://msdn.microsoft.com/en-us/library/system.linq.enumerable.sum(v=vs.110).aspx
Enumerable.Range Method (System.Linq) (2016, March 22). Retrieved from: https://msdn.microsoft.com/en-us/library/system.linq.enumerable.range%28v=vs.100%29.aspx?f=255&MSPPError=-2147217396
Davis, E. (2012). Linear Algebra and Probability for Computer Science Applications. United States: CRC Press.

V