Tabla de Contenido
0. Introducción1. Conversión en Sistemas Numéricos
2. Complemento (~)
3. AND (&)
4. OR Inclusivo (|)
5. OR Exclusivo (^) - XOR
6. Desplazamiento a la Izquierda
7. Desplazamiento a la Derecha
8. Conclusiones
9. Glosario
10. Referencias
Introducción
En esta entrada veremos una introducción generalizada acerca de los operadores bitwise (bit a bit) que provee C#. Estos operadores son muy interesantes debido a aspectos como rendimiento y eficiencia en el consumo de poder por parte de los circuitos integrados de un sistema de cómputo pequeño. Además, y de acuerdo con [2]: en procesadores de bajo coste, las operaciones bitwise son mucho más eficiente y rápidas que la división, e inclusive varias veces más rápidas que la adición, la substracción y la multiplicación, debido a que son tratadas directamente por las instrucciones de bajo nivel sobre el procesador adyacente.
A pesar que muchos de los procesadores modernos incluyen diseños más óptimos que igualan o superan con operaciones aritméticas a las operaciones bitwise, muchas veces programadores o diseñadores de circuitos deben enfrentarse a retos de rendimiento sobre dispositivos con procesadores de bajas prestaciones (sinónimo de procesadores para fines específicos, por ejemplo, un sistema embebido que requiera bajo poder de cómputo para poder funcionar); entonces es necesario pensar en operar a nivel de bit con los operadores que le corresponde que conduzcan a bajo de consumo de poder por parte del dispositivo.
En la Tabla 1 vemos el listado de operadores bitwise que soporta el lenguaje de programación C#.
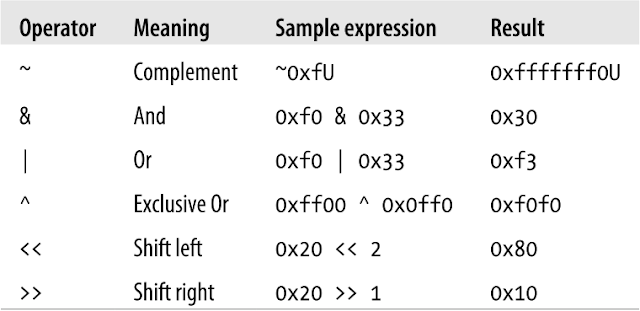 |
| Tabla 1. Operadores bitwise en C# [3]. |
1. Conversión de Sistemas Numéricos
Antes de pasar a demostrar el uso de los operadores bitwise de C#, es importante introducir el concepto de conversión y las operaciones o pasos necesarios para llevar un número de un sistema de numeración a otros (e.g., decimal) a otro distinto (e.g., binario [1]). Además esto nos ayudará entender la utilidad de estos operadores y lo interesante que resultan para proyectos de hardware.
El sistema de numeración decimal nos resulta muy familiar pues es el universalmente utilizado para muchas aplicaciones de la vida diaria: mercado, academia (involucradas las matemáticas), en las rutinas diarias, el tiempo, etc. Este sistema está compuesto por 10 cifras diferentes (de ahí su nombre) y los números se componen y generan el significado de acuerdo a su posición. Ejemplos de números decimales:
Por otro lado, el sistema de numeración binario es el lenguaje de las computadoras para tomar decisiones y procesar datos. Los programas y operaciones escritas en este lenguaje para los humanos resulta complejo y dispendioso para completarse. Los mismos tres números anterios en base decimal, ahora en binario:
1.1 Decimal a Binario
Este proceso de conversación es muy sencillo, consiste en realizar divisiones sucesivas: empezando por el número en base decimal dividido por 2; el residuo de esta división puede ser 0 ó 1, este valor va formando parte de la cadena de bits de la conversión resultante, el cociente se convertirá en el divisor (debe ser distinto a 0) por 2. El proceso anterior finaliza cuando el cociente de la división iterativa se convierta en cero.
Para ilustrar con más detalle este proceso se presenta la Tabla 2.
Tabla 2. Conversión 495 (base decimal) a binario (base dos).
Entonces asumamos que en C# el número 495 se almacena en una variable tipo Int16 [4], luego su equivalente en binario es: 111101111.
Para convertir un número decimal negativo (e.g., -495) a binario, seguimos el siguiente proceso:
Para convertir un número decimal negativo (e.g., -495) a binario, seguimos el siguiente proceso:
- Tomamos la representación binaria de 495: 111101111.
- Lo invertimos: 000010000.
- Le sumamos 1: 000010001.
- Luego como el tipo de dato es Int16 rellenamos los bits restantes con el signo para negativo, es decir 1, así: 1111111000010001.
1.2 Binario a Decimal
Pasemos a convertir un número en base dos a base diez: 0000111100000111 (Int16) . Obsérvese que el primero dígito es 0 por lo tanto el número es negativo). Ahora, este número lo representamos en su modo inverso, así: 1110000011110000. Ahora utilicemos el siguiente método (Tabla 3):
Ahora procedemos a sumar todos los resultados de la tercera fila:
1 + 2 + 4 + 0 + 0 + 0 + 0 + 0 + 256 + 512 + 1024 + 2048 + 0 + 0 + 0 = 3847
Adicionalmente, podemos agregar el proceso de conversión de un número binario negativo a decimal (1111111111010011 (Int16), observemos que se trata de un número negativo, pues el bit más significativo es 1):
Tenamos en cuenta que si el tipo de dato es con signo:
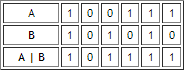
Tenemos los números decimales 17 y 29. Los convertimos en binario y tenemos:
Apliquemos el operador XOR (^):
Cuando operamos A ^ B obtenoms 1100 (12 en decimal).
Esta misma operación en C#:
Archivo C# OperadorXOR.cs [enlace alternativo]:
La operación 7 << 2 mueve 2 bits a la izquierda sobre 7 (00000111). Observemos esta operación para diferentes número de desplazamientos a la izquierda en la siguiente tabla:
Obsérvese que a medida que se agregan ceros (0) a la izquierda el número binario puede ocurrir dos casos:
1 << n calcula 2^n. Esta operación bitwise resulta mucho más rápida que la función estática Math.Pow. Mirémoslo en el siguiente ejemplo en C#:
Archivo C# DesplazamientoIzquierdaPotenciasDeDos.cs [enlace alternativo]:
En la siguiente tabla se va representado fila por fila el cambio efectuado a medida que aumenta el número de bits de desplazamiento a la derecha sobre el decimal 160:
Ejemplo básico en C#:
Archivo C# DesplazamientoDerecha.cs [enlace alternativo]:
Archivo C# RendimientoDesplazamientoDerecha.cs [enlace alternativo]:
 |
| Tabla 3. Conversión Binario a Decimal. |
1 + 2 + 4 + 0 + 0 + 0 + 0 + 0 + 256 + 512 + 1024 + 2048 + 0 + 0 + 0 = 3847
Adicionalmente, podemos agregar el proceso de conversión de un número binario negativo a decimal (1111111111010011 (Int16), observemos que se trata de un número negativo, pues el bit más significativo es 1):
- Invertimos el número original: 0000000000101100.
- El anterior número en decimal es igual a 44.
- Sumamos 1 a 44: 45.
- Lo convertimos a negativo: -45.
- Entonces 1111111111010011 equivale a -45 en decimal.
2. Complemento (~)
El operador bitwise ~ -o NOT-, realiza la operación unaria que ejecuta la negación lógica de cada bit del número binario en cuestión. Si en la cadena de bits encontramos un 1 esté será 0, si por el contrario hayamos un 0 se convertirá en 1.Tenamos en cuenta que si el tipo de dato es con signo:
- Si el número es negativo se convertirá en positivo:

- Si el número es positivo se convertirá en negativo:

Código ejemplo en C#:
byte b = 53;
Console.WriteLine("{0:0}", Convert.ToString(b,2));
byte notB = (byte)~b;
Console.WriteLine("{0:0}", Convert.ToString(notB,2));
En byte notB = (byte)~b; se declara la variable notB de tipo byte y asignamos el complemento de b. En la salida estándar:
Convirtamos los dos siguientes números a binario, 113 y 121:
Aplicando el operador & a los dos números binarios resultantes, tenemos:
Entonces, cuando operamos 1111001 AND 1110001 obtenemos: 1110001 (113 en decimal).
Cuando operemos A & B:
Archivo C# OperadorAND.cs [enlace alternativo]:
byte b = 53;
Console.WriteLine("{0:0}", Convert.ToString(b,2));
byte notB = (byte)~b;
Console.WriteLine("{0:0}", Convert.ToString(notB,2));
En byte notB = (byte)~b; se declara la variable notB de tipo byte y asignamos el complemento de b. En la salida estándar:
- Console.WriteLine("{0:0}", Convert.ToString(b,2)); muestra en pantalla 110101. La clase estática Convert [] posee varios métodos miembro estáticos para la conversión entre tipos numéricos.
3. AND (&)
El operador & corresponde con la operación lógica AND (conjución lógica [6]). Vamos a realizar la siguiente operación utilizando este operador para dejar más claro el concepto:Convirtamos los dos siguientes números a binario, 113 y 121:
Aplicando el operador & a los dos números binarios resultantes, tenemos:
Entonces, cuando operamos 1111001 AND 1110001 obtenemos: 1110001 (113 en decimal).
Cuando operemos A & B:
- Si A y B son negativos el resultado de operar A & B será negativo,
- En caso contrario, el resultado será positivo.
Archivo C# OperadorAND.cs [enlace alternativo]:
4. OR Inclusivo (|)
Para ejecutar una operación de este tipo, también realizamos la conversión de decimal a binario. Aquí tenemos un ejemplo con dos números decimales: 39, y 42. El equivalente en binario:
Cuando operamos bit a bit con este operador, el resultado es 0 cuando ambos operandos son 0, y 1 en para los dos casos restantes. Miremos el resultado de operar 1000111 | 101010:
Entonces, al operar A | B obtenemos 101111 (equivalente a 47 en decimal).
Equivalente en C#:
5. OR Exclusivo (^) - XOR
A excepción de del OR inclusivo, este operador genera como resultado 1 cuando ambos operandos son diferentes (de ahí su nombre). Hagamos un ejemplo para demostrar el uso de este operador:Tenemos los números decimales 17 y 29. Los convertimos en binario y tenemos:
Esta misma operación en C#:
Archivo C# OperadorXOR.cs [enlace alternativo]:
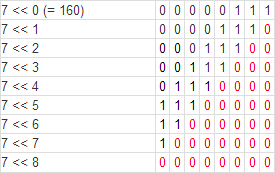
6. Desplazamiento a la Izquierda <<
Con esta operación bitwise, podemos mover n cantidad de bits a la izquierda sobre x: x << n. Las posiciones vacías se rellenan con ceros. Ver Figura 1 (tomada desde [7]):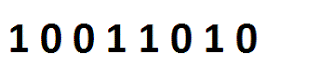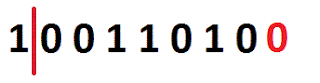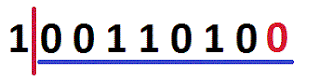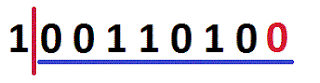 |
| Figura 1. Desplazamiento a la Izquierda [7]. |
Obsérvese que a medida que se agregan ceros (0) a la izquierda el número binario puede ocurrir dos casos:
- El número aumente de valor como en 7 << 1, 7 << 2, y 7 << 3, o que
- El número disminuya su valor como 7 << 6, 7 << 7, y 7 << 8.
Ahora pasemos a mirar esta operación en lenguaje C#:
Archivo C# DesplazamientoIzquierda.cs [enlace alternativo]:
Archivo C# DesplazamientoIzquierda.cs [enlace alternativo]:
Cálculo de potencias de 2 usando desplazamiento a la izquierda
A continuación también se demuestra uno de los beneficios de usar operaciones bitwise a sus homólogas aritméticas.1 << n calcula 2^n. Esta operación bitwise resulta mucho más rápida que la función estática Math.Pow. Mirémoslo en el siguiente ejemplo en C#:
Archivo C# DesplazamientoIzquierdaPotenciasDeDos.cs [enlace alternativo]:
7. Desplazamiento a la Derecha >>
Con esta operación bitwise, podemos mover n cantidad de bits a la derecha sobre x: x << n. Las posiciones vacías se rellenan con ceros. Ver Figura 2 (tomada desde [7]):Nota
Si el tipo de dato numérico posee signo, éste será conservado a pesar del desplazamiento.En la siguiente tabla se va representado fila por fila el cambio efectuado a medida que aumenta el número de bits de desplazamiento a la derecha sobre el decimal 160:
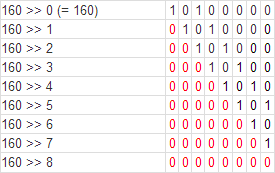 |
| Tabla. Desplazamiento a la derecha sobre 160. |
Archivo C# DesplazamientoDerecha.cs [enlace alternativo]:
Cálculo de x / 2^n usando Desplazamiento a la Derecha
Al usar x >> n es equivalente a x/2^n. Por ejemplo, 3 >> 2 equivale a 3 / 2^2 (3/4). Esta operación también resulta más rápida que 2/Math.Pow(2,3). Veámoslo en el siguiente ejemplo:Archivo C# RendimientoDesplazamientoDerecha.cs [enlace alternativo]:
8. Conclusiones
En este artículo pudimos enunciar algunas de las ventajas (e.g., rendimiento sobre procesadores de bajo poder de procesamiento o de bajo coste) de los operadores de bitwise. También se introdujeron ejemplos sencillo acerca del cómo las operaciones desplazamiento a la izquierda (left shift) y desplazamiento a la derecha (right shift) son mucho más eficientes que las aritméticas.
9. Glosario
- Binario- Decimal
- Desplazamiento a la derecha (right shift)
- Desplazamiento a la izquierda (left shift)
- Operación bitwise
- Sistema numérico
10. Referencias
[1] Binary number - http://en.wikipedia.org/wiki/Binary_numeral_system[2] Bitwise operation - http://en.wikipedia.org/wiki/Bitwise_operation
[3] C# 5.0 in a Nutshell by Joseph Albahari and Ben Albahari. Copyright 2012 Joseph Albahari and Ben Albahari, 978-1-449-32010-2.
[4] C# Int16, Int32 and Int64 Types - http://www.dotnetperls.com/int16-int32-int64
[5] Convert Class - http://msdn.microsoft.com/en-us/library/system.convert(v=vs.71).aspx
[6] Conjunción lógica - http://es.wikipedia.org/wiki/Conjunci%C3%B3n_l%C3%B3gica
[7] Understand how bitwise operators work (C# and VB.NET examples) - CodeProject - http://www.codeproject.com/Articles/544990/Understand-how-bitwise-operators-work-Csharp-and-V#exclusiveor
J










No hay comentarios:
Publicar un comentario
Envíe sus comentarios, dudas, sugerencias, críticas. Gracias.